The electron impact ionization cross sections in the ELIIXS database are calculated using the Modified Relativistic binary-encounter Bethe (MRBEB) model [1]. This model is a modification of the RBEB model [2], which combines the Mott cross section with the high incident electron’s kinetic energy behavior of the Bethe cross section within the relativistic framework. The MRBEB does not use any fitting parameters, and provides a simple analytic formula for the ionization cross section per atomic orbital.

The ionization cross section for a given atomic orbital nlj, in reduced units, is given by

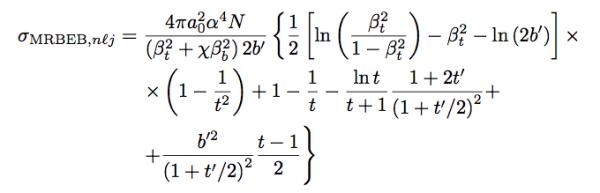where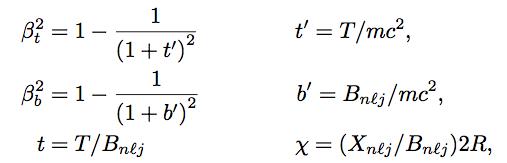

and T is the incident electron’s kinetic energy, U and Bnlj are the target electron’s kinetic and binding energies respectively. The N parameter is the occupation number of the orbital under ionization, R is the Rydberg energy (13.6 eV), a0 is the first Bohr radius, α is the fine structure constant, c is the speed of light in vacuum, and m is the electron mass. It is assumed that all the energy values are in the same units and a0 is in the SI system. Xnlj is a scaling factor given by

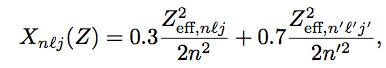where Zeff is the effective nuclear charge that accounts for the electronic shielding and electronic correlation, and n′l′j′ stands for the orbital immediately after the nlj orbital in the energy scale. The scaling factor Xnlj for the last occupied orbital nlj should be written as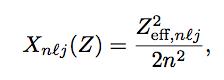meaning that for the outer shells the penetration of the incident electron upon ionization, in this model, is much higher than for inner-shells as expected.

In the cases where the Zeff is not known, we may use the well-known approximation that considers the effective nuclear charge to be given by the atomic number minus the inner electrons up to the sub-shell being ionized,

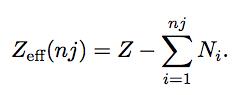
The MRBEB expression is valid for all shells of elements with atomic number ranging from Z = 3 (Lithium) to Z = 92 (Uranium).

In order to calculate total ionization cross sections σTotal for neutral elements or ions, we need only to sum the contributions from all active shells nlj, i.e.,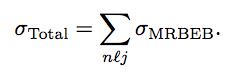All the electronic structure parameters necessary to evaluate the MRBEB expression were calculated with the Multiconfiguration Dirac-Fock General Matrix Elements code of J. P. Desclaux and P. Indelicato [3, 4]. Details of the method can be found, for instance, in References [5, 6].

References
[1]  M. Guerra, F. Parente, P. Indelicato, and J. P. Santos, International Journal of Mass Spectrometry 313, 1 (2012).
[2]  Y.-K. Kim, J. P. Santos, and F. Parente, Physical Review A 62, 052710 (2000).
[3]  J. P. Desclaux, Computer Physics Communications 9, 31 (1975).
[4]  P. Indelicato and J. P. Desclaux, Physical Review A 42, 5139 (1990).
[5]  P. Indelicato, Physical Review A 51, 1132 (1995).
[6]  I. P. Grant, H. M. Quiney, B. David, and B. Benjamin, in Advances in Atomic and Molecular Physics (Academic Press, Volume 23, pp. 37–86, DOI: 10.1016/S0065-2199(08)60105-0.